软光栅渲染器（三） Hidden faces removal (z buffer)

前言

上节课我们实现了三角形的光栅化，但是在渲染整个模型时，可以看到有很多不知道怎么形容的错误，即使我们没有使用正确的纹理，我们能看出来它的结构有很大的问题，只是因为我们错误渲染了很多应当被隐藏的面。

Z-Buffer算法用于解决这一问题。

---

Painter’s algorithm

如果我们将所有的三角形排序后渲染，那么后渲染的三角形理所应当会覆盖之前绘制的三角形，我们就可以看到一个正常显示的模型。

但是这么说起来还是太理想了，有下面几个问题：

1. 如何对三角形进行排序？仅仅按照z最大值/平均值或者其他关键字？
2. 如何处理三角形相交的问题？如果三角形A的一部分被B遮挡，而三角形A的另一部分遮挡了B，画家算法可以绘制出正确的图像吗(如下图，来源于tinyrenderer wiki)？

除了上面两个影响正确性的问题，画家算法伴随着高昂的计算成本。对于动态场景/静态场景内视角变化，我们需要每次重新对三角形排序。

Depth interpolation

深度插值并不是直接解决伪影的办法，它可以看作z-buffer的理论基础。在上节课，为了判断像素点是否在三角形内，我们得到了每个点的重心坐标。我们根据 $\alpha,\ \beta,\ \gamma$ 将像素点的颜色插值为三角形点的z坐标加权和，即：

#pragma omp parallel for
	for(int x = minx; x <= maxx; ++x) {
		for(int y = miny; y <= maxy; ++y) {
			Point p(x, y);
			float alpha = signed_area(p, p1, p2) / total_area;
			float beta 	= signed_area(p0, p, p2) / total_area;
			float gamma = signed_area(p0, p1, p) / total_area;
			unsigned char z = alpha * p0.z + beta * p1.z + gamma * p2.z;
			if(alpha < 0 || beta < 0 || gamma < 0) continue;
			zbuffer.set(x, y, {z});
			img.set(x, y, color);
		}
	}

我们可以绘制深度图像如下:

可以从图片上看出伪影还是很严重的。

Per-pixel painter’s algorithm (a.k.a. z-buffer)

看看下面一段代码：

#pragma omp parallel for
	for(int x = minx; x <= maxx; ++x) {
		for(int y = miny; y <= maxy; ++y) {
			Point p(x, y);
			float alpha = signed_area(p, p1, p2) / total_area;
			float beta 	= signed_area(p0, p, p2) / total_area;
			float gamma = signed_area(p0, p1, p) / total_area;
			unsigned char z = alpha * p0.z + beta * p1.z + gamma * p2.z;
			if(alpha < 0 || beta < 0 || gamma < 0) continue;
			if(zbuffer.get(x, y)[0] >= z) continue;
			zbuffer.set(x, y, {z});
			img.set(x, y, color);
		}
	}

效果：

可以看到运行结果有了极大的改善。为什么？

在深度插值算法中，我们对于每个三角形中的每个像素计算了一次深度。我们可以把这个深度存在一张单独的图片（zbuffer）中。在下一次计算这个像素的深度值时，我们将新的深度与buffer中的深度作比较，只有当zbuffer.get(x, y)[0] < z时才更新这个像素。

我们用同一套程序，还是随机填色，来更新上节课渲染的模型：

已经看不到伪影了。

作业：Texture

ssloy大神在v1的wiki中在这一章布置了添加纹理的作业，并提供了纹理贴图。

在obj格式模型以f开头的行，形如f 1/2/3 4/5/6 7/8/9中，我们之前使用的1 4 7为点坐标，而2 5 8对应的就是纹理坐标。

在模型读取函数中稍作修改，并保存每个三角形顶点的纹理坐标，那么只需要用同样的插值方法，我们就可以得到每个像素点对应的uv坐标。将这个uv坐标映射到纹理图像坐标上，可以取到纹理图像中的一个像素点，这个像素点就是最终的填色。

获取这个颜色的代码：

float u = p0.u * alpha + p1.u * beta + p2.u * gamma;
float v = p0.v * alpha + p1.v * beta + p2.v * gamma;
int tx = u * (texture.width() - 1);
int ty = v * (texture.height() - 1);

img.set(x, y, texture.get(tx, ty));

运行效果：

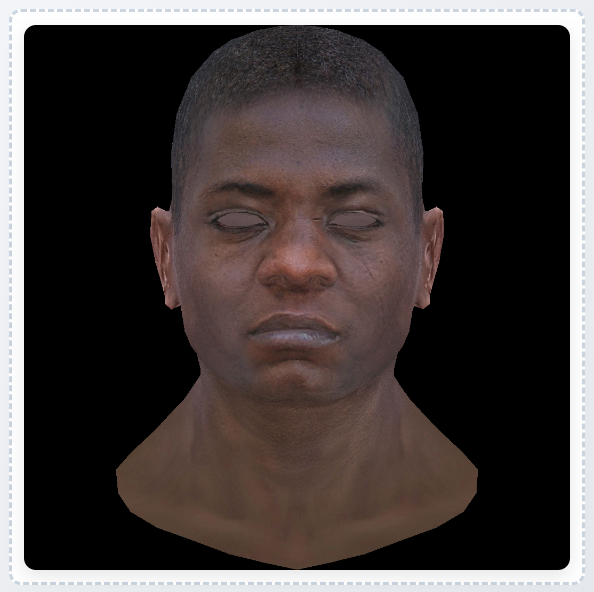
我们得到了比较完美的图像（他看上去没有眼睛，但实际上ssloy大神提供的模型就是没有眼睛的）。